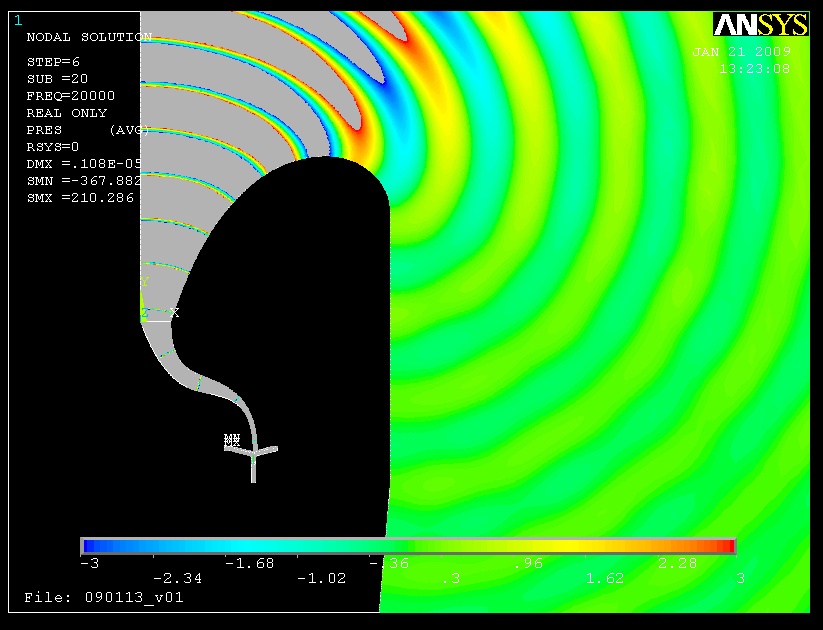
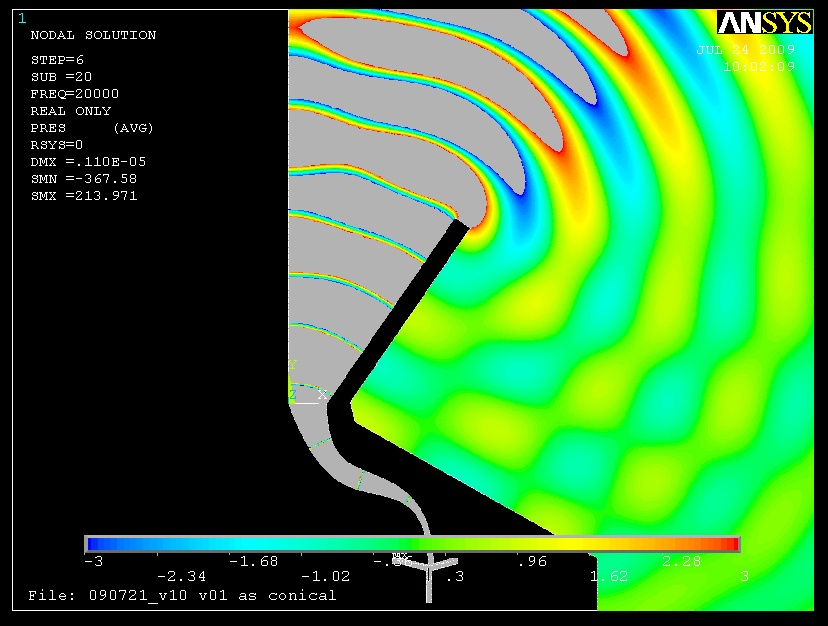
I got into a discussion on an audio discussion board about the differences between a LeCleac'h horn and a conical horn without a mouth flair. So I presented some data to illustrate some of the performance differences and thought I'd post the same data here on my website. On to the data - I dug up some old FEA results to show a typical scenario. These are from a fully coupled model. In other words, the diaphragm, suspension, coil, phase plug, etc. of the driver are modeled along with the interaction of those elements with the air. The electrical / magnetic portion of the driver is included as a lumped element model. This simulation is from a 2kHz horn for a JBL 2402 ring radiator. The same driver / phase plug is used for both scenarios - only the horn is different. The conical horn is approximately the same size as the Le Cleac'h horn (it was drawn over the LC horn). This simulation has proven very accurate for directional effects. In other words while the frequency response may be off a bit from reality, the response at 0 degrees, 10 degrees, etc. will all be off in exactly the same way, and thus looking at normalized polar responses or directivity indexes will give an accurate prediction of reality. This has been tested many times using real parts in a calibrated, NIST traceable test system in an anechoic chamber. Also, if you wanted to extrapolate these results to a lower frequency range, you could expect the effected frequency range to be proportionately lower. For example if you were interested in a 200hz horn, the effect seen in these simulations at 10kHz would be seen at 1kHz. Here are screen shots of both models at 20kHz to show the geometries under discussion. The color scale shows pressure in a steady state anechoic environment. The scale is set to show primarily waves outside the horns, but you can also see the shape of the wavefronts in the horn. The grey color is where the pressure goes above the upper limit of the scale. Note that the phase plug for the 2402 is not the JBL plug.
First, let's look at the normalized response curves every 10 degrees from 0 to 180 degrees for a 2kHz t=1.4 Le Cleac'h horn. These values are taken at a 1m distance from the throat of the driver. If you eq'd the on-axis response of the horn to dead flat (the line at 0dB), then all the response curves at the various angles would be as shown in this chart. Although there are differences in the on-axis response of various horns, this method levels the playing field in that regard (since you could, and arguably should, equalize the horn in the design of the crossover). What we are looking for are similar response curve shapes as we move off axis. Ideally, at least if we wanted constant directivity, we would see flat lines but at decreasing levels as we moved off axis. What we don't want to see is changing response shapes at various angles, as this will screw up the spectrum of the reflected sound.
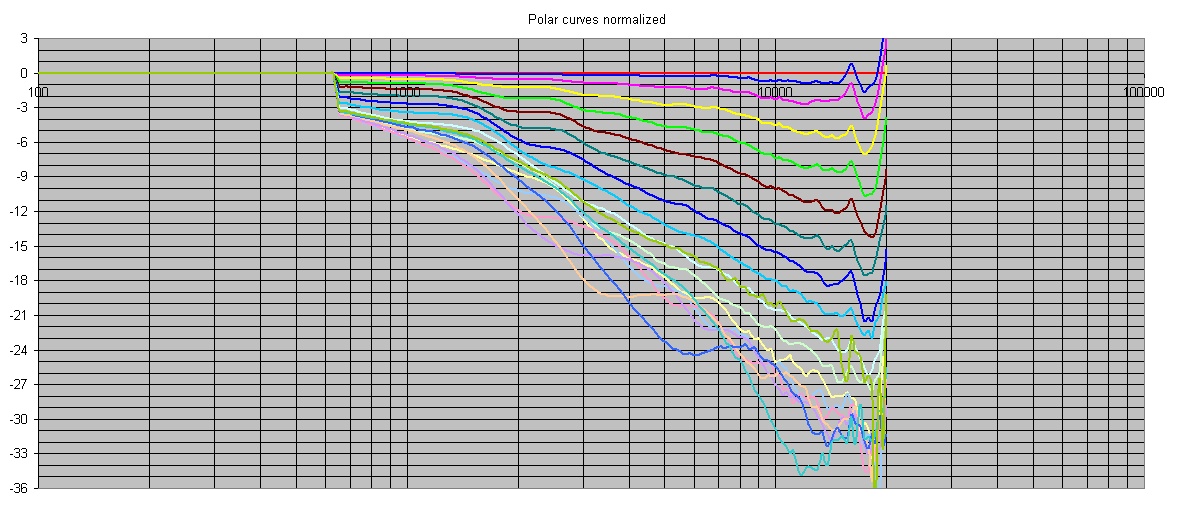
So what we see in the LeCleac'h curves are that the responses are all similar except for 3 at the very bottom that have a few bumps in them. These are 140, 150 and 160 degrees from on axis.
Now let's look at the same curves for a straight conical horn with no mouth round over. These look decidely less orderly. You can see there's a big dip around 9kHz in the 50, 60 and 70 degree curves (brown, green, blue), but then the 80 degree curve (magenta) and the lower curves don't have this dip. Also, this dip is above 10kHz in the 40 degree curve (light green) and maybe a little higher in frequenc in the 30 degree curve (yellow), although it's tough to say if that's the same effect or not because it's less pronounced. Also, notice the dip in all the curves at around 3khz. Now notice how this dip progress from ~3kHz at angles close to on axis to ~4kHz as the angle moves further off axis. Lastly, lets look at the 10kHz to 20kHz region. Notice the chaotic behaviour from one curve to the next. There's a second notch that starts to crop up in the middle of that frequency range but is absent in some curves and moving around in frequency in curves where it is present.
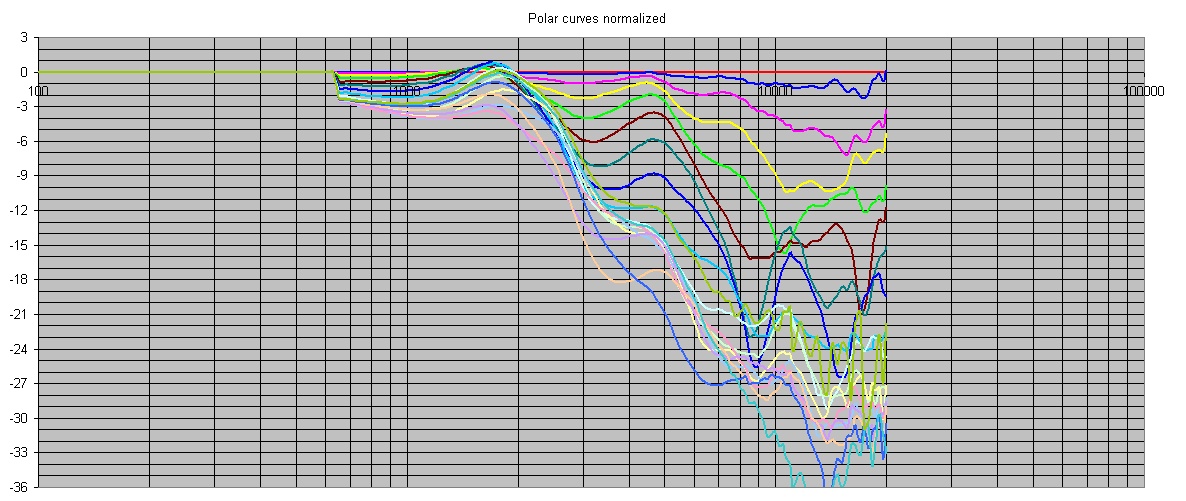
Basically all this is not good. It means that no matter how you eq the horn, the response will never be uniform or even close to uniform at all angles - the spectrum of the reflected sound will always be different than the direct sound. While the Le Cleac'h horn is not constant directivity, the spectrum of its reflected sound will at least be a simple smooth rolloff of the highs (which is very typical for speakers as almost all speakers increase their directivity at high frequencies). Whether that smooth rolloff is desirable is debatable, but if you don't want it then the solution is an OS waveguide with a round over at the mouth.
Now let's look at the same data in another way - directivity index. Directivity index shows how directional a speaker is. A directivity index (DI) of 0 is an omnidirectional speaker - it radiates the same in all directions, or at least averages out to doing so. A 3dB DI would be a speaker that radiates only into half space. What the DI can show us is how directive a speaker is and how that changes with frequency. It's an easier measure to look at than the raw response curves to get a quick idea of how the speaker's going to image, how and where to cross it over and to what speaker you might cross it to. Once again, we'd like to see a smoothly changing DI. For constant directivity, the DI would be flat versus frequency.
Below we see a chart showing the DI for both the Le Cleac'h and the conical. Note the low end of the frequency range (~2kHz). For the Le Cleac'h, DI smoothly changes from about 4dB at 1.4kHz to 12dB at 12kHz. Now notice that the conical horn has a DI of almost zero around 1.7kHz and then rapidly rises, falls again, and then rises at a faster rate than the LeCleac'h horn before plateauing around 9kHz. Since this is the range you'd likely cross over to this horn (3-4kHz), this is where you'd like a smoothly changing DI. While all horns will have their DI decrease at the low end of their range as they become acoustically small relative to the wavelengths being produced, if they do this smoothly it will be easier to match up their directivity to the device working in the frequency range below them as there will be more overlap of the DI's. This is really what we want - a smooth transition to the next driver. This keeps the spectral balance even in the reflected energy. The oft cited example of a big offender in this category is crossing a very small dome tweeter at a relatively low frequency to a large woofer at a relatively high frequency for the woofer, as this causes a large jump in the DI. The woofer will have significant direcitivity at the top end of its frequency range while the small tweeter will be omnidirectional at its low end. This is what we're trying to avoid.
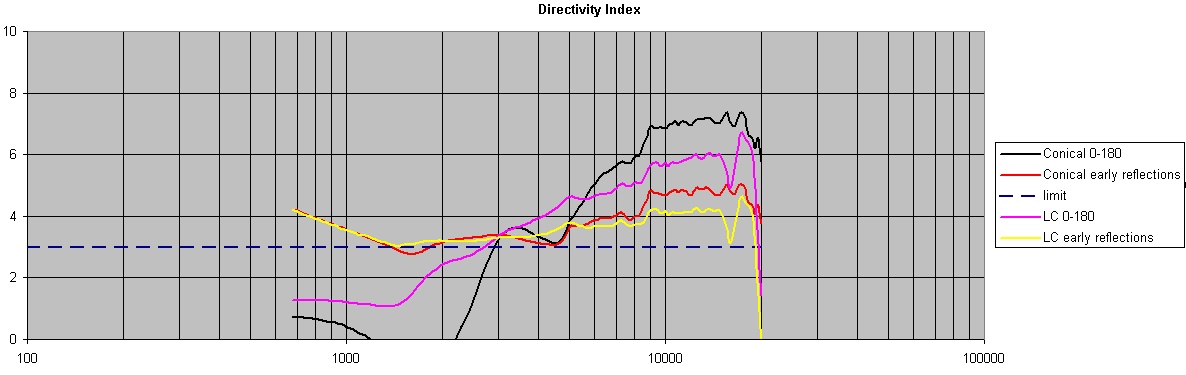
Now look at the early reflection DI curves in the above graph. These curves show the DI but only looking at 0 to +/-30 degrees horizontal and 0 to +/-10 degrees vertically. Although I have not heard of a completed study on this, this measure should show what the imaging will be like. Once again, the Le Cleac'h is smoother and flatter - DI does not rise as much at high frequencies.
In both these curves, the advantage of the conical is that once it becomes acoustically large, the DI is somewhat smoother. This is seen above 10kHz - the LeCleac'h has the dip in DI at 16kHz while the conical does not. The Le Cleac'h also has a dip in DI at 20kHz, but because this is the very top end of the simulation, I would not put as much confidence in this. The element size in my model might have gotten a bit too large.
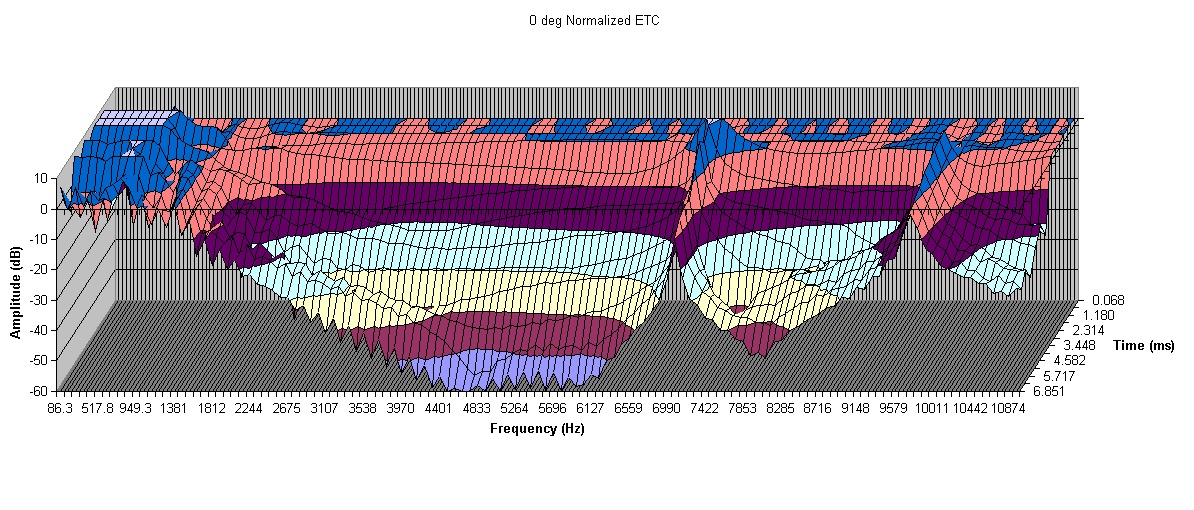
Now let's look at data from a transient analysis. A force was applied to the voice coil and then removed in the time span of one sample at 44.1kHz. The acoustic pressure was recorded for ~10ms with a 44.1kHz sampling rate following this impulse at points at every 10 degrees around a 1m arc as above. This data was then processed to produce energy time curves which are displayed as a normalized (the response is flattened) waterfall plot. Note that these plots are displayed on a linear frequency scale which isn't great, but it's a limitation of Excel. Also note that I have an overlayed line plot of the response at various times that I'm using to pick off frequencies and levels, but it's kind of confusing to look at on its own so I'm just showing the waterfall. Anyway, let's look at the on-axis waterfall for both horns.
Below is the waterfall plot for the Le Cleac'h horn. Notice it generally decays smoothly at a somewhat constant rate in the middle of its range. It makes it down to -60dB in ~7ms in the 4-6kHz range. It has resonances at ~7kHz and 10kHz. In the 8kHz to 10kHz range, there is a dip and then the level rises back up (to the left of the 10kHz resonance ridge). It also does this to a lesser degree below 3kHz. Ideally we'd like it decay smoothly, quickly, without resonances, and not bounce back up in level at any frequency, but we'll take this performance as our baseline - decaying well in the middle of the horn's bandwidth and not quite as well at the upper and lower extremes.
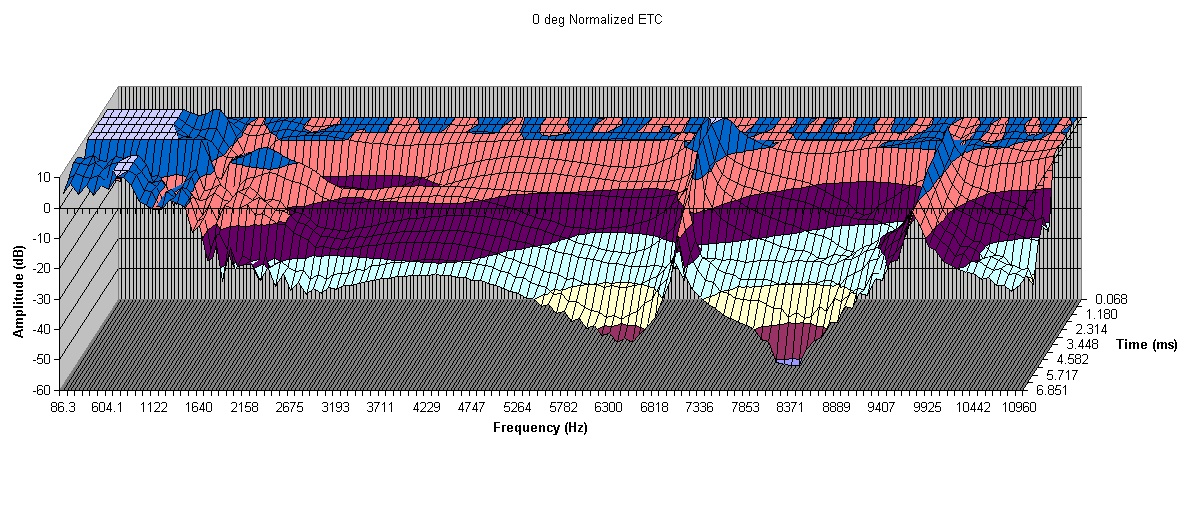
Now let's look at the same waterfall plot for the conical with no mouth termination. What we see first are the same resonances at 7kHz and 10kHz. This probably means they're caused by the driver. But we see a much smaller amount of decay in the 3kHz to 6kHz range in the same time as compared to the LeCleac'h horn. While the Le Cleac'h horn decays to -60dB, the conical only gets down to -25 to -30dB in the same period of time. Beyond this interpretation becomes somewhat subjective in my opinion, as there are pros and cons in other frequency ranges for both dvices, but I would note that the conical appears to decay better between the two resonances around 8kHz.
Also, while it could be argued (in the absence of data) that some of these effects are just the conical flair versus the Le Cleac'h flair, I would add that I have also simulated a comparable OS waveguide with a mouth radius and it does not have the problems this conical does - polar response is smooth and decay performance is much closer to the LeCleac'h.
These are just some of the issues caused by not having a mouth radius. Other issues might include production of more higher order modes. Also, if there isn't a smooth transition out of the driver at the throat, this will cause even more HOM's. Read Geddes to find out more about this. There have been tons of discussions on diyaudio about this for the last year or so. He has identified this as the cause of horn sound - waves bouncing around inside the horn and reemerging later as delayed energy.
Having said all this, please understand I'm not saying that conical horns with no mouth termination sound horrible. From my previous systems on my webpage, I've obviously listened to quite a few and they can sound pretty good. However if we're looking at horn systems for home usage, especially large horns it's obvious we're neurotically pursuing the last little bit of sonic performance. And these issues are much more than just the last little bit of performance - I'd say they're at least moderately significant.








